Secrets in the Stones: Decoding Anglo-Saxon Art. Part 4

Early Anglo-Saxon jewellery is renowned for its use of gold and garnet work. Until now, the significance of garnets as a material has not been thoroughly investigated. In this article, and a public lecture at Soulton Hall, Shropshire (delivered simultaneously with this article’s timed release) James D. Wenn draws together the geometry of the garnet crystal with the geometry within Anglo-Saxon art and architecture, signposting to the previous articles in this series. This is then coupled with later examples of this geometry, notably the Cosmati Pavement in Westminster Abbey, to link the philosophical meaning of this geometry to Plato’s book ‘Timaeus’, and both pre-Christian and Christian cosmology and theology.
|
Copyright and citations notice
The synthesis between observations made in this article is the intellectual property of James D. Wenn and Byrga Geniht Ltd. The form of words is copyright James D. Wenn and Byrga Geniht Ltd, 2023. Pictures, diagrams and links remain property of their respective copyright holders. Licences may be sought for use of Byrga Geniht Ltd images and text by contacting Byrga Geniht Ltd. Thegns of Mercia hold a permanent licence for use of Byrga Geniht Ltd text and images within this article. Thegns of Mercia is the publisher of this article. Citations of this article must reference James D. Wenn and Thegns of Mercia, and link to this article or reproduce its URL. |
Author
James D. Wenn holds an MA in Anglo-Saxon, Norse and Celtic from the University of Cambridge, and an MA in The English Country House from Leicester University. He is a trustee of the Essex Cultural Diversity Project, and founder of Byrga Geniht consultancy. He has been a member of the Thegns since 2019.
|
Introducing the Garnet
The natural rhombic-dodecahedral form of the garnet is shown in the attached photograph of the author at a Thegns of Mercia event at Sutton Hoo in 2022. The specimen shown was mined in Africa, but we know that the garnets used in the Sutton Hoo and Staffordshire Hoard jewellery derived from central Europe and India.
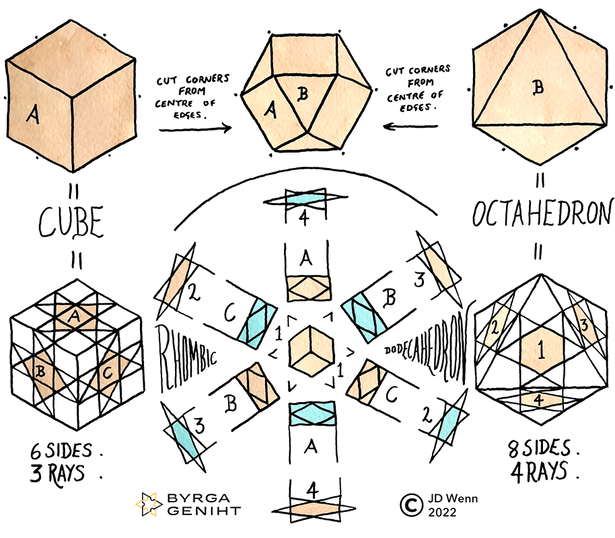
The linked video shows how a rhombic dodecahedron can be made out of two cubes. If you pull apart one of the cubes by its six square faces, you find each face carries with it a pyramid of material that narrows into the centre. In other words, you can make a cube out of six identical square-based pyramids.
The ratio of each face is a width of value one, to a length of the square root of two. A way to intuit why this ratio includes the square root of two takes us back to the ‘pyramid method’ of constructing a rhombic dodecahedron. Let each edge of the initial cubes measure 1. The edges of the pyramids around the square base therefore also measure 1. The apex of each pyramid was once the centre of the cube. So, if we take a line from the middle of an edge of the original cube to the centre, this is the same as taking a line from the apex to the middle of the edge at the base of a pyramid. If we extend this line through the cube past the centre to the middle of the opposite edge of the cube, this is the same as the length of one of the rhombuses/lozenges on the rhombic dodecahedron. A cross section of the cube would be a square with a diagonal corner-to-corner line, making two identical right-angled triangles. As each triangle is right-angled, we can apply Pythagoras’ Theorem — the first short edge squared, plus the second short edge squared, equals the long edge (the hypotenuse) squared — as follows: (1x1)+(1x1)=2. The hypotenuse thus measures the square root of 2, and so does the route through the cube, and the length of the rhombus in the rhombic dodecahedron.
Now imagine we have a stack of cubes, with all their faces and edges lined up. Take one cube within the stack, and divide it into six pyramids (without moving anything). Attach each of these pyramids to the cube whose square face touches it. Then take these new solids, and similarly divide-then-attach the five other cubes that touch each of them, so that they also become rhombic dodecahedra. Repeat the process. This should make it clear how identical rhombic dodecahedra can be used to fill a three-dimensional volume without gaps. It may help to think of this like a 3D chess board where each dark cube is the core of a rhombic dodecahedron, and each white cube provides one pyramid to each adjoining dark cube.
From six directions (perpendicular to the faces of the ‘inner cube’ cube) a rhombic dodecahedron has a tilted square silhouette (projection), and shows four of its faces (the apex of one pyramid and the sides of four others). From eight directions (looking directly at the corners of the ‘inner cube’) a rhombic dodecahedron has a hexagonal silhouette, and shows three of its faces (arranged around the cube’s corner). This happens to be a way in which bees often cap the end of honeycomb.
Also of note is that in four spatial dimensions the rhombic dodecahedron is called a hyperdiamond, and becomes a Platonic Solid in this dimension. Platonic Solid is the name traditionally given to something whose edges and angles are all identical. A rhombic dodecahedron has identical faces and identical edges, but there are two different angles involved in its faces. It takes an extra spatial dimension to give space to allow these to become identical. It is probable that the rhombic dodecahedron’s exclusion from the 3D Platonic Solid list (described in Euclid’s ‘Thirteen Books of the Elements’, Book 13) has led to its unfamiliarity with today’s public.
Establishing the Anglo-Saxons knew of the rhombic dodecahedron
The remainder of the faces of the rhombic dodecahedron which the Maldon holy water sprinkler models have bars that trace the long and short (length and width) paths between the vertices of the object (and the corners of the lozenges). The relationship of these, as has been discussed, is a ratio of one to the square root of two, but there is another mathematical significance that can help locate the Maldon object in a wider field of contemporary material culture.
The link between these solids causes us to take the ubiquity of the cuboctahedron in Roman and Anglo-Saxon jewellery more seriously than has hitherto been the case. Pins described as ‘polyhedral’ or ‘faceted-headed’ occur in both Roman and early Anglo-Saxon contexts, but become the predominant type of dress-pin across Britain during the eighth century, coinciding with the development of lozenge-brooches. The heads of these pins are most commonly cuboctahedral. Examples include SUR-A551E7 from Hampshire, YORYM-F9D484 from York and KENT-F499EE from Kent.
Partial examples

In Secrets in the Stones Part 2 (available here) Ædmund Thompson comprehensively explores the weight placed on the lozenge shape (and the tilted square shape) in Anglo-Saxon art and architecture. The lozenge represents one face of the rhombic dodecahedron, whilst the tilted square relates to either its internal geometry or to its methods of construction. The cross-within-lozenge motif (like faces of the Maldon holy water sprinkler) seen across Anglo-Saxon art thus represents the relationship between the cube, octahedron, tetrahedron and square pyramid via the rhombic dodecahedron.
We decided to invest in the articles leading to this one to speed up the grand reveal in this article, but they were written in full knowledge if the conclusions reached here.
A more complex geometry in millefiori

 Author with a scaled-up replica of the millefiori apices of Staffordshire Hoard pyramids Cat 578 & Cat 579. Lecture prop produced by glass specialist Caroline Weidman, Wiedman Glass, Essex
Author with a scaled-up replica of the millefiori apices of Staffordshire Hoard pyramids Cat 578 & Cat 579. Lecture prop produced by glass specialist Caroline Weidman, Wiedman Glass, Essex
The design is likely therefore to have been of importance, considering the pains taken to achieve it. Ignoring the geography of the current art glass scene, the likelihood the glass was of Anglo-Saxon manufacture (or focused on an Anglo-Saxon market) is enhanced by comparisons with the millefiori work in the Sutton Hoo treasure, in particular in the shoulder clasps, where the same design of nine grid and Xs can be seen, but made from different glass canes.
This star-like pattern is popular in Latvia, and is known as the Auseklis. Owing to its having been found there in prehistoric contexts, it is something of a national symbol. It is beyond the scope of this article to examine international links relating to the symbol, but from here the shape will be referred to as the Auseklis.
Returning to an earlier section of this article, we can reflect how in our 3D chessboard, the Staffordshire Hoard Auseklis gives a helpful cross section of rhombic dodecahedra filling 3D space, as well as a guide to constructing one by projecting a tilted square through each face of a cube, as shown in the videos below.
Likewise, Cat 580 & 581 have an X in gold amid garnets at its flat apex, and this appears to be an important shape. Added to these, the Sutton Hoo Mound 1 sword pyramids (BM 1939,1010.28 & 29) have 25 grid chequerboards which gain significance in spite of not displaying Xs.
Most of these examples date from the early conversion period (the first quarter of the seventh century CE), with some such as the Sutton Hoo Mound 17 examples predating the mission of St Augustine (597 CE) therefore evidencing pre-Christian Anglo-Saxon engagement with these concepts.
An extremely explicit example of the X shape grouping in fours to delineate a tilted square is found on a gold shilling found near Harrogate in 2012 (EMC number 2012.0025). The monarch for whom it was minted is not recorded on the coin, but a date range is given of 600 to 867 CE. The obverse shows a stylised bearded man (perhaps Christ or an evangelist) standing between two long crosses.
Looking at the geometric proofs (diagrams and videos) in this article, we can see how the use of the Auseklis on each side of a cube can be used to project tilted square rays or beams. Four Xs are required on each of the six faces of the cube, and this gives a total of 24 (the number of runes in the Elder Futhark). The choice within the runic system to employ a word associated with time to a device used to construct the rhombic dodecahedron is something to note, considering the later history of this geometry in English art.
A thirteenth-century Anglo-Saxon revival
At Westminster Henry constructed a coronation theatre centred on a square pavement (known as the Cosmati Pavement) at whose centre is the spot where the act of coronation has taken place ever since Henry’s second coronation on 17 May 1220.
Thinking about projecting beams of light forming a rhombic dodecahedron leads us to consider the Westminster Retable (a richly decorated piece of sculptured board amusingly described as a sort of splashback to the altar table). There is more information about this on the website for Westminster Abbey (here), where it is on display in the Queen’s Diamond Jubilee Galleries.
The upper portion of the central section contains mosaic work in red and blue glass. Blue octagons separate red tilted squares that would glint and shine down the length of the abbey. The attached video shows how this pattern is also a cross section of a volume filled with rhombic dodecahedra.
 'Scutum fidei' / Shield of Faith (Public Domain)
'Scutum fidei' / Shield of Faith (Public Domain)
There is an allegorical implication in this geometry that the unity of God is experienced as a Trinity according to the projection along which God is approached, and this may have influenced the famous ‘scutum fidei’ (shield of faith) heraldic device which depicts God named in the centre, and three bands (labelled ‘est’ (is)) connecting the three persons of the Trinity (The Father, The Son, and The Holy Spirit). The coronation theatre is therefore geometrically described as being a concentrated or focused holy place, via art and architecture. The late mediaeval coronation is therefore something of a communion with the divine more akin to Pentecost than baptism, but containing the same demand for a special place.
Unlocking the Anglo-Saxon world through Henry III’s revival
The first thing to note is that as soon as the idea has been understood that the groins or ribs of a vault can be connected to an important geometric symbolism in defining the division of space beneath, Repton’s nine grid gains the Xs that define a large tilted square that penetrates between its famous four spiralled columns.
The second thing to note is how a unique feature of the design of Westminster’s Cosmati Pavement is its use of thick, dark Purbeck marble bands delineating the design. Whilst it is now clear how this feature helps the readability of the Auseklis, the origin of the aesthetic has not been very clearly explained in the literature around the pavement. At Repton, however, the surviving floor is very sunken, irregular and uneven, but with a level (dark) stone sill around part of the edge of the room. Could it be that the floor once had a mosaic pavement of the kind that was consistently being produced in the Mediterranean world at that time? Part of the presentation of the mosaic theory for the original floor treatment at Repton is the idea that Henry III or his designers visited Repton specifically looking for inspiration. This article asserts the theory that this event did occur ‒ that the Cosmati Pavement is a direct evocation of Repton as part of Henry III’s Anglo-Saxonism.
The third thing to note is that the average measurement given in the literature for the internal dimensions of the crypt is 16 feet by 16 feet. This measurement corresponds with the inner square of the Cosmati Pavement.

If these niches are, however, windows, we again see ecclesiastical architecture creating opportunities for light to intersect at 90 degrees, imbuing the central part of the space with a special glow that the dark corners of the room (where the crypt is entered) would not have.
Oddly this arrangement is also reminiscent of the sword pyramids.

 Effigy, tomb of Henry III with tilted-square-on-square cushion arrangement (CC. Valerie McGlinchey. Wikimedia Commons)
Effigy, tomb of Henry III with tilted-square-on-square cushion arrangement (CC. Valerie McGlinchey. Wikimedia Commons)
Pictorial or symbological representation of a building via a birds-eye-view plan was known to the early Anglo-Saxons, as evidenced by the plan of the Temple of Solomon in the Codex Amiatinus, produced in Jarrow in the late seventh century.
The garnets potentially represent beams of red light coming in from the sides of a cube, complementing the tilted square in the millefiori glass that gives us the vertical dimension (like the Cosmati Pavement does). Incidentally, this gives rise to our wondering about the iconography of the red cross in the evangelists’ portrait page in the eighth-century Lichfield Gospels, as well as the Flag of the Resurrection (red cross on white field) that become used as a badge in the time of Henry III and eventually became associated with St George and England itself.
A fifth thing to note is the tomb of Henry III ‒ how it potentially corroborates these observations with its combination of spiralled columns and panelled pilasters, along with its continuation of the same rich geometry in its mosaic work, and the striking fact of a square and tilted square cushion arrangement supporting the head of the royal effigy (a trend repeated by the tomb of Edward III on the other side of the sanctuary).
A philosophical reading
The chief foundation of this is the set of inscriptions in the pavement. (Details and visiting information may be found here.)
In the year of Christ one thousand two hundred and twelve plus sixty minus four, the third King Henry, the city, Odoricus and the abbot put these porphyry stones together.
If the reader wisely considers all that is laid down, he will find here the end of the primum mobile; a hedge (lives for) three years, add dogs and horses and men, stags and ravens, eagles, enormous whales, the world: each one following triples the years of the one before.
The spherical globe here shows the archetypal macrocosm.
Christian theology sees God as existing outside of the constraints of linear time by which we, as mortals, are bound. So, a person viewing the Cosmati Pavement has a view representing the way God sees both time and space ‒ all spread out at once, crystallised in eternity. If each piece of the mosaic represents a person (their soul), we see the individuality of people in their different shapes and colours. The limits of a piece represent a mortal person’s limits both in space and in time. The different patterns in the different mosaic panels of the pavement thus represent different social contract organisations (kingdoms, civilisations ancient, present and future). At this zoomed-in scale, however, they are crudely symbolic ‒ the number of people anyone knows massively outstrips the number of stones adjoining one another directly. Even so, the pavement as a whole is bewildering in its complexity. It confronts a monarch at the moment of coronation with the sublime reality of God’s view, compared to their own relative inadequacy.
The rhombic dodecahedron is a Platonic Solid (a perfect shape) in four spatial dimensions (where it is called a hyperdiamond), and it is a reasonable technique of art to represent time allegorically using this extra spatial dimension. If you were to drop a ball through a 2D plane, somebody inhabiting that 2D world would see a line grow from a point and then diminish as the 3D ball passed through. Going around it, they would perceive that the object was circular, but the way it appeared, grew, diminished and vanished would appear very odd. If a 4D person dropped a 4D ball through our three dimensions, we would see a ball swell from nothing, diminish, then vanish. If a 4D person dropped the hyperdiamond ‒ this special Platonic Solid ‒ through our three dimensions, we would see a rhombic dodecahedron swell from nothing. This swelling effect is echoed in the Cosmati Pavement inscription, and the obsession with threes makes sense given the 3x3 nature of the nine grid used to conceptualise a hovering volume of space that could represent some substance from the world of the 4D person ‒ God in the Kingdom of Heaven ‒ that might equate to some notion of Divine Grace or a visitation by the Holy Spirit in the manner of the light or fire of Pentecost.
The connection of space and time (cosmology) with the rhombic dodecahedron is likely anchored by Plato’s work known as ‘Timaeus’. It is very necessary to take a long passage from Desmond Lee’s translation:
In the first place it is clear to everyone that fire, earth, water and air are bodies, and all bodies are solids. All solids are again bounded by surfaces, and all rectilinear surfaces are composed of triangles. There are two basic types of triangle, each having one right angle and two acute angles: in one of them these two angles are both half right angles, being subtended by equal sides, in the other they are unequal, being subtended by unequal sides. This we postulate as the origin of fire and the other bodies, our argument combining likelihood and necessity; their more ultimate origins are known to god and to men whom god loves. We must proceed to inquire what are the four most perfect possible bodies which, though unlike each other, are some of them capable of transformation into each other on resolution. If we can find the answer to this question we have the truth about the origin of earth and fire and the two mean terms between them; for we will never admit that there are more perfect visible bodies than these, each in its type. So we must do our best to construct four types of perfect body and maintain that we have grasped their nature sufficiently for our purpose. Of the two basic triangles, then, the isosceles has only one variety, the scalene an infinite number. We must therefore choose, if we are to start according to our own principles, the most perfect of this infinite number. If anyone can tell us of a better choice of triangle for the construction of the four bodies, his criticism will be welcome; but for our part we propose to pass over all the rest and pick on a single type, that of which a pair compose an equilateral triangle. It would be too long a story to give the reason, but if anyone can produce a proof that it is not so we will welcome his achievement. So let us assume that these are the two triangles from which fire and the other bodies are constructed, one isosceles and the other having a greater side whose square is three times that of the lesser. We must now proceed to clarify something we left undetermined a moment ago. It appeared as if all four types of body could pass into each other in the process of change; but this appearance is misleading. For, of the four bodies that are produced by our chosen types of triangle, three are composed of the scalene, but the fourth alone from the isosceles. Hence all four cannot pass into each other on resolution, with a large number of smaller constituents forming a lesser number of bigger bodies and vice versa; this can only happen with three of them. For these are all composed of one triangle, and when larger bodies are broken up a number of small bodies are formed of the same constituents, taking on their appropriate figures; and when small bodies are broken up into their component triangles a single new figure may be formed as they are unified into a single solid.
So much for their transformation into each other. We must next describe what geometrical figure each body has and what is the number of its components. We will begin with the construction of the simplest and smallest figure. Its basic unit is the triangle whose hypotenuse is twice the length of its shorter side. If two of these are put together with the hypotenuse as diameter of the resulting figure, and if the process is repeated three times and the diameters and shorter sides of the three figures are made to coincide in the same vertex, the result is a single equilateral triangle composed of six basic units. And if four equilateral triangles are put together, three of their plane angles meet to form a single solid angle, the one which comes next after the most obtuse of plane angles: and when four such angles have been formed the result is the simplest solid figure, which divides the surface of the sphere circumscribing it into equal and similar parts.
The second figure is composed of the same basic triangles put together to form eight equilateral triangles, which yield a single solid angle from four planes. The formation of six such solid angles completes the second figure.
The third figure is put together from one hundred and twenty basic triangles, and has twelve solid angles, each bounded by five equilateral plane triangles, and twenty faces, each of which is an equilateral triangle.
After the production of these three figures the first of our basic units is dispensed with, and the isosceles triangle is used to produce the fourth body. Four such triangles are put together with their right angles meeting at a common vertex to form a square. Six squares fitted together complete solid angles, each composed by three plane right angles. The figure of the resulting body is the cube, having six plane square faces.
There still remained a fifth construction, which the god used for embroidering the constellations on the whole heaven.
(Plato's Timaeus. Translation by Desmond Lee)
Since the fifth 3D Platonic Solid is the pentagonal dodecahedron, and since Roman dodecahedra have been archaeologically described, as mentioned above, it has been widely assumed that Plato referred to this when he wrote of the ‘fifth construction’. However, the speculations in ‘Timaeus and Critias’ relating to cosmology are tied to Plato’s meditations on a perfect society (and the allegorical story of Atlantis, for which this work is chiefly known).
The rhombic dodecahedron can fulfil a role similar to that of the ashlar cube in the allegory of Freemasonry. That is, if the stone represents a person, they can fit together in a perfect society as a ‘polished’ character, just as cubes can fit together and fill volumes. Yet the rhombic dodecahedron is more subtle, as it has both square and hexagonal projections, so one may need to be manipulated to find the right fit. Earlier I described how visualising a 3D chessboard may help in grasping the way this 3D tessellation works from the square projections mindset. From a different angle, the rhombic dodecahedra fit together like layers of honeycomb, offset to mesh together. The use of bees as social allegory is seen in both Anglo-Saxon and Frankish society, and has classical roots (for example, throughout Virgil’s Georgics, Book IV). The fertile ground for Plato’s social philosophy that the rhombic dodecahedron offers lends weight to our identification of his fifth solid at least as much as the observation that whereas garnet crystals commonly grow as rhombic dodecahedra, pentagonal dodecahedra are vanishingly rare in nature.
In a previous article in this series (here) I demonstrated evidence of knowledge of Plato’s ‘Timaeus’ and Ptolemy’s ‘Harmonics’ in the Sutton Hoo scabbard bosses. The present discussion is an area in which the ramifications of that work may bear substantial fruit.
The Cosmati Pavement places a heavy emphasis on the four hexagonal projections of the rhombic dodecahedron. We can see evidence of earlier engagement with hexagonal geometry in the ninth-century triumphal arch or gatehouse at the imperial abbey at Lorsch in Germany. Built in white and red stone, the parquetry of the facade follows Roman mosaic work and prefigures later lapidary work such as at Westminster Abbey.
The use of the hexagram connects the ninth-century work at Lorsch directly to the culture of the Staffordshire Hoard and Sutton Hoo Auseklis glasswork. As shown in the attached diagram and videos, the treatment of the cube with the Auseklis can be mirrored by treating the connected octahedron in the same way. A division of its edges into thirds, and the connecting of these points with parallel lines, gives a hexagram whose inner hexagon will be a projection of the exact same rhombic dodecahedron as that produced by its twin using the Auseklis on the cube. Mere knowledge of projections of a rhombic dodecahedron would not offer up the hexagram as a preferred symbol.
Having reached this theory through Anglo-Saxon jewellery evidence, and not just through architecture, Henry III’s view of Repton as a coronation site can be thought of as reasonable, although the early jewellery evidence suggests that whilst broad concepts may have longevity, surface aesthetics may impede cultural legibility. The coronation we will witness in 2023 will not closely resemble any seventh-century initiation rituals to leadership, even though we are beginning to understand the strength of philosophical and liturgical continuity.
Conclusion and epilogue
The millefiori glass in the Staffordshire Hoard and Sutton Hoo combines with the Maldon holy water sprinkler and the Rhenish Helm roofs to cement the rhombic dodecahedron as a significant piece of intellectual freight that holds substantial explanatory power within Anglo-Saxon (and Frankish) art and architectural history. This fundamental form is naturally embodied in an explicit way by whole garnets, and in a symbolic (or occult) manner by use of this material.
Our new understanding of this geometry, and its central role in the meaning of thirteenth-century English coronation liturgy, opens up a greater understanding of the survival or resurrection of Anglo-Saxon intellectual, spiritual and/or artistic impulses beyond the Norman Conquest.
In the other direction, increased appreciation for the philosophical connections between the Anglo-Saxons’ hitherto unexplained love for garnets and ancient and classical philosophy and science opens up avenues into questioning Roman continuity, international connections, and other topics in early Anglo-Saxon studies.
Through the interpretive possibilities presented by Plato’s ‘Timaeus’, we can begin to examine how philosophy through geometric allegories may have informed the aesthetics of status and social organisation through a very long period of history. This is a vast field that has only just been opened.
As we prepare for a coronation this year, on the Cosmati Pavement and according to long-observed ritual, we may reflect on what impact this art history (outlined only briefly in this article) has had upon the intervening centuries of English culture: what has evolved and how. I am preparing a book for publication this year, which has examined this later history in great depth, including moments of unexpectedly intense Anglo-Saxon artistic revival in places as diverse as the Tudor Soulton Hall in Shropshire, the works of Sir Christopher Wren, Newgate Prison, and government buildings in England and the USA.
Acknowledgements
Additionally the Thegns of Mercia family as a whole has been immensely supportive during this period, and thanks also go to the many contacts in my network who have encouraged me and permitted access to resources and locations of importance in this research, both in terms of discovering things and ruling things out.
It would also be appropriate to again signal my thanks and respect to the university departments of my education years ago — to the Department of Anglo-Saxon, Norse and Celtic at the University of Cambridge, and The Centre for the Study of the Country House at Leicester University.
Resources
Fern, C., T. Dickinson and L. Webster, eds., The Staffordshire Hoard: an Anglo-Saxon treasure (London, 2019)
Heath, T.L., trans. and ed., Euclid: the thirteen books of the elements (New York, 1956), 3 vols.
i Altet, X.B., The Early Middle Ages: from Late Antiquity to AD 1000 (Cologne, 2002)
Lee, D., trans. and ed., Plato: Timaeus and Critias (London, 1965)
Mortimer, P. ‘The riddle of the pyramids: An attempt to unravel their meaning. A typology and comments on chronology’. Mortimer, P. & Bunker, M. The sword in Anglo-Saxon England: from the 5th to 7th century (Ely, 2019)
Rodwell, W., and D.S. Neal, The Cosmatesque Mosaics of Westminster Abbey (Oxford, 2019)
Taylor, H.M. and J. Taylor, Anglo-Saxon Architecture (Cambridge, 1965), 2 vols.
Archaeology Data Service, Staffordshire Hoard: archaeologydataservice.ac.uk/archives/view/staffshoard_he_2017
Fitzwilliam Museum, Cambridge: emc.fitzmuseum.cam.ac.uk
Portable Antiquities Scheme: finds.org.uk
- Clifford, T (2006) "SUSS-3C8EA4: A MEDIEVAL STAFF" Web page available at: https://finds.org.uk/database/artefacts/record/id/128035 [Accessed: 13 Apr 2023]
- Fittock, M (2019) "BH-692011: A ROMAN DODECAHEDRON" Web page available at: https://finds.org.uk/database/artefacts/record/id/941889 [Accessed: 13 Apr 2023]
- Maslin, S (2022) "SUR-A551E7: A EARLY MEDIEVAL PIN" Web page available at: https://finds.org.uk/database/artefacts/record/id/1084705 [Accessed: 13 Apr 2023]
- Rogerson, L (2022) "KENT-F499EE: A EARLY MEDIEVAL PIN" Web page available at: https://finds.org.uk/database/artefacts/record/id/1090156 [Accessed: 13 Apr 2023]
- Rivett, A (2022) "YORYM-F9D484: A EARLY MEDIEVAL PIN" Web page available at: https://finds.org.uk/database/artefacts/record/id/1088729 [Accessed: 13 Apr 2023]
- Scott, W (2011) "LEIC-15A132: A EARLY MEDIEVAL MOUNT" Web page available at: https://finds.org.uk/database/artefacts/record/id/467984 [Accessed: 13 Apr 2023]
Westminster Abbey: westminster-abbey.org
Further Information
Byrga Geniht on YouTube: youtube.com/@ByrgaGeniht
Forthcoming publication:
J.D. Wenn, Stones of the Magi: the history of magic in English stately architecture (London, expected 2023)




















 RSS Feed
RSS Feed
